在查看本文之前，请先思考两个问题。

typeof (1 / undefined) 是多少
[1,2,NaN].indexOf(NaN) 输出什么

如果你还不确定这两题的答案的话，请仔细阅读本文。这两题的答案不会直接解释，请从文章中寻找答案。

NaN 的本质

我们知道 NaN(Not A Number) 会出现在任何不符合实数领域内计算规则的场景下。比如 Math.sqrt(-1) 就是 NaN，而 1 / 0 就不是 NaN。前者属于复数的范畴，而后者属于实数的范围。

同时需要注意的是，NaN 只会出现在浮点类型中，而不会出现在 int 类型里（当然 JS 并没有这个概念）

什么意思？用你熟悉的任何支持 int 和 double 两种类型的语言（比如 C）。在保证它不会偷偷做隐式类型转换的情况下，分别用 int 和 double 打印出 sqrt(-1)，你就能发现只有在 double 的类型下才能看到 NaN 出现，而 int 呢？编译器甚至会给你一个 Warning。

那么在浮点数下是如何表示一个 NaN 的呢？为了方便，下面用单精度 float 来表示，请看下图。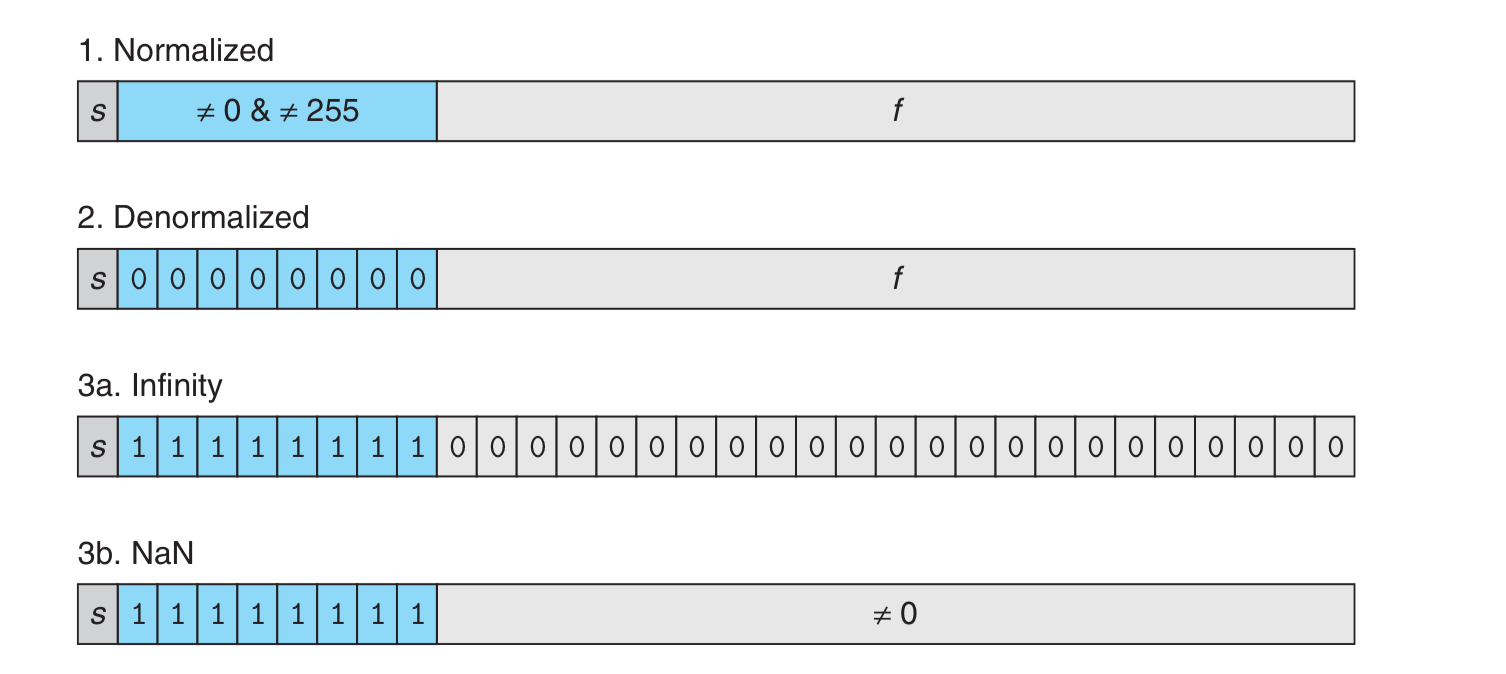在 3b 情况中，NaN 得满足：从左到右，以 1 开始，不关心第 1 位的值，第 2 位到第 9 位都是 1，剩下的位不全为 0。 关于浮点数内部的组成，这里不做具体的介绍，我们只需要了解到浮点数分为 3 个部分就可以：

符号位
指数位
精度位

其中 float 的指数位有 8 位，精度位有 32 - 1 - 8 = 23 位 double 的指数位有 11 位，精度位有 64 - 1 - 11 = 52 位
所以上面 NaN 的满足条件，可以看成：精度位不全为 0，指数位全 1 就可以了。

所以按上面的说法，0x7f81111, 0x7fcccccc 等等这些都符合 NaN 的要求了。我们可以尝试一下，自己写一个函数，用来往 8 个字节的内存的前两个字节写入全 1. 也就是连续 16 个 1，这就符合 NaN 的定义了。看下面这段代码：

double createNaN() {  
  unsigned char *bits = calloc(sizeof(double), 1);
  // 大部分人的电脑是小端，所以要从 6 和 7 开始，而不是 0 和 1
  // 不清楚概念的可以参考阮老师：
  // [理解字节序 - 阮一峰的网络日志](http://www.ruanyifeng.com/blog/2016/11/byte-order.html)
  bits[6] = 255;
  bits[7] = 255;
  unsigned char *start = bits;

  double nan = *(double *)(bits);
  output(nan);
  free(bits);
  return nan;
}

其中 output 是一个封装，用来输出任意一个 double 的内部二进制表示。详细代码查看 gist。最后我们得到了：

看来创造一个 NaN 不是很难，对吧？同样的，为了证明上面的图的正确性，再看看 Infinity 的内部结构是否符合

两种 NaN

如果再细分的话，NaN 还可分为两种：

Quiet NaN
Signaling NaN

从性质上，可以认为第一种 NaN 属于“脾气比较好”，比较“文静”的一种，你甚至可以直接定义它，并使用它。比如我们在 JS 中可以使用类似于 NaN + 1, NaN + '123' 的操作，还不会报错。

而 Signaling NaN 就是一个“爆脾气”。如果你想直接操作它的话，会抛出一个异常（或者称为 Trap）。也就不允许 NaN + 1 这种操作了。像这种不好惹的 NaN，根据 WiKi 中的介绍，它可以被用来：

Filling uninitialized memory with signaling NaNs would produce the invalid operation exception if the data is used before it is initialized Using an sNaN as a placeholder for a more complicated object , such as: A representation of a number that has underflowed A representation of a number that has overflowed Number in a higher precision format A complex number

NaN != NaN

如果换个角度理解，因为 NaN 的表示方式实在太多，仅仅在 float 类型中，就有 2^(32-8) 中情况，所以 NaN 碰到一个和它二进制表示一模一样的概率实在太低了，所以我们可以认为 NaN 不等于 NaN 😏

嗯。看上去似乎问题不大，但是我们都知道计算机在大多数情况下，都是按规矩办事，这种玄学问题肯定不是内部的本质吧？要是真这样，世界上每一个程序员同时输出 NaN === NaN，总有一个人会得到 true，然后他就到 stackoverflow 上发了一个帖：你看 NaN 其实是会等于 NaN 的！ 但我们从来没有见过这样的帖子，所以计算机内部肯定不是用这种颇为靠运气的方式在处理这个问题。

考虑换一种方式，假设计算机内部是通过位运算来判断的。如果某一个数的内部结构满足第 2 位到第 9 位全 1，剩下的 22 位不为 0，那它就是 NaN。我们可以这样写

_Bool isnan(double whatever) {  
  long long num = *(long long *)(&whatever); // 浮点数不能进行位运算，所以要改成整数类型，同时保留内部的二进制组成
  long long fmask = 0xfffffffffffff; // 不要数了，13 个 f，52 个 1
  long long emask = 0x7ff; // 11 个 1
  num <<= 1;
  num >>= 1; // 清除符号位
  return ((num & fmask) != 0) && (((num >> 53) & emask) == emask);
}

你可以试着把这段 C 代码运行一下，配合上面的 createNaN 可以试一下，他是真的可行的！

接着要实现 NaN != NaN 的特性，只需要在每次 == 的时候进行检测：只要有一个操作数是 NaN，那么就返回 false。

实际情况下的 NaN != NaN 的实现

那么实际情况到底是怎样的呢？不同的系统会有不同的实现。

在 Apple 实现的 C 库的头文件中，可以看到，nan 在 float 下，仅仅就是一个数，它等于 0x7fc00000，也就是 0b0111 1111 1100 0000 0000 0000 0000 0000，符合上面的 NaN 的定义。 #define NAN __builtin_nanf("0x7fc00000") 而它们的 isnan 的实现也相当简单

#define isnan(x)    \
    (sizeof (x) == sizeof(float)    ?  __inline_isnanf((float)(x))  \
  :  sizeof (x) == sizeof(double)  ?      __inline_isnand((double)(x))  \
    :   __inline_isnan ((long double)(x)))

static __inline__ int __inline_isnanf( float __x ) {  
    return __x != __x;
}
static __inline__ int __inline_isnand( double __x ) {  
    return __x != __x;
}
static __inline__ int __inline_isnan( long double __x ) {  
  return __x != __x;
}

仅仅只是简单的判断自己是否等于自己 🌚。在 C 中具体如何实现 x !== x，有两种可能：

硬件支持 NaN 异常，所以永远都是 false
像下文中提到的 V8 的实现方式

而在 V8 中，分为两个阶段：/Compile Time and Runtime/。

在 Compile Time，编译器如果在代码中碰到了 NaN 常量，就会自动将替换成 NaN 对应的那个常量，比如上文提到的 0x7fc00000。因为编译器已经明确知道了谁是 NaN，所以在写出形如 NaN === NaN 这种代码的时候，就能直接得到 false。

而在 Runtime 阶段，不是用户直接定义的 NaN，比如下面代码：

const obj = { a: 1, b: 2 };  
let { c, d } = obj;  
c *= 100;  
d *= 100;  
console.log(c === d);

这种情况下，我们虽然一眼可以看出最后的 c 和 d 都是 undefined，但是编译器刚开始不知道，所以它只能在最后判等的时候，才能得到结果。而具体判断的逻辑如下图所示：我们先检查，操作数是否有 NaN，如果有？那就返回 false 吧

所以 Number.isNaN 的 polyfill 可以怎么实现呢？

Number.isNaN = function(value) {  
  return value !== value;
}

就是这么简单 😎

参考文献

欢迎关注我们的公众号