基于时间加权的用户购买类目意愿计算
背景
在DMP的人群画像或者商品画像等的应用中，有一类常见的打分需求 旨在基于一些transactions，为两种关系打上一个归一化的分数 比如基于一个用户的购买商品行为对该用户购买类目意愿打分，该文章讨论如何在考虑时间因素的情况下给用户打分
要求
- transaction发生的时间越近，其所占的比重越大,且减小的速度越来越慢
- 所有分数都需要正则化到0-100区间
数据形式:
输入的数据(表示某人某天买了某个类目多少单): 用户id 日期 类目id cnt
最终产出数据：
用户id 对每个类目的购买意愿分
实现方式
- 第一点要求'transaction发生时间和现在的距离'越小，这条记录越大，
就像一个热门事件，会被人慢慢遗忘，且后续遗忘的速度越来越慢
基于这个需求，很容易让人想到基于热力学的牛顿冷却定律
牛顿冷却定律: 物体的冷却速度，与当前温度与室温之间的温差成正比
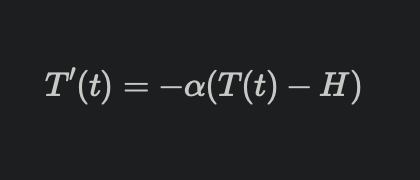换成数学语言表达就是
其中H为室温
初始时刻的温度为
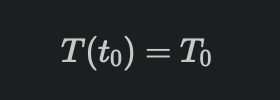其中 alpha > 0 为与物体有关的常数,为负数表示当物体温度高于室温的时候，物体温度会下降，但当物体温度低于室温的时候会上升
对于上个公式:
两边取积分:
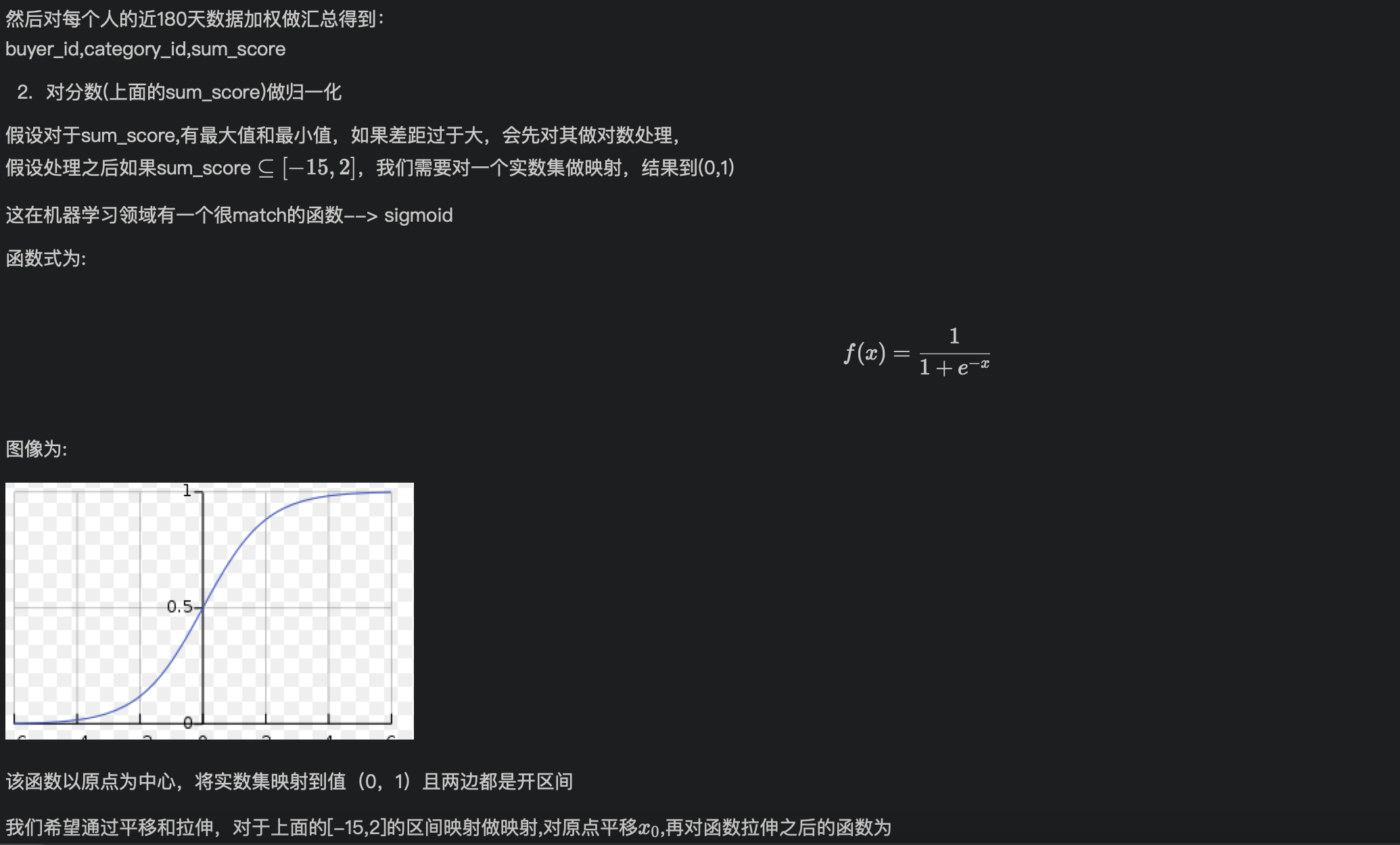
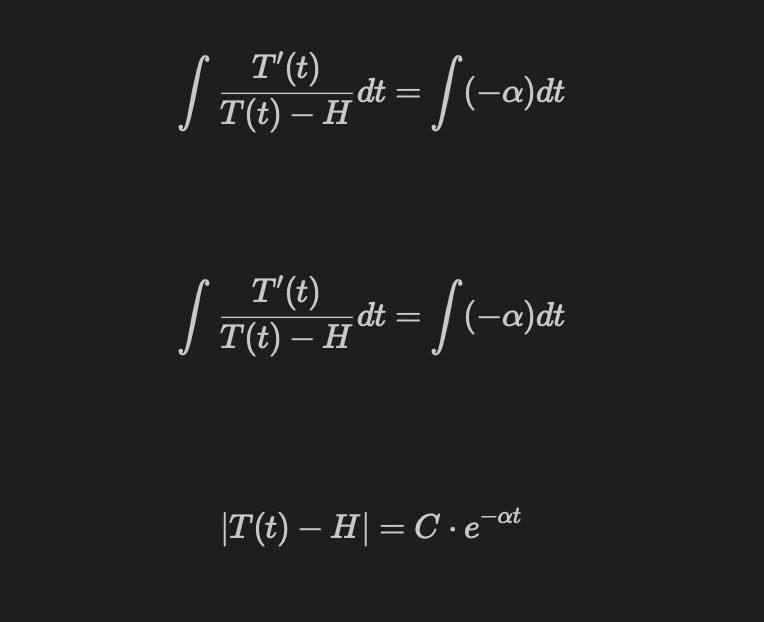带入 T(t0) = T0
可以得到
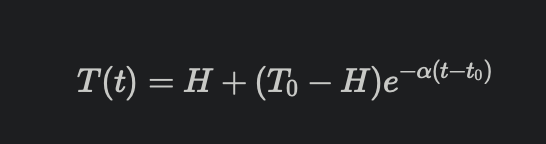
然后对每个人的近180天数据加权做汇总得到：
buyerid,categoryid,sum_score
- 对分数(上面的sum_score)做归一化
假设对于sumscore,有最大值和最小值，如果差距过于大，会先对其做对数处理， 假设处理之后如果sumscore $\subseteq [-15, 2]$，我们需要对一个实数集做映射，结果到(0,1)
这在机器学习领域有一个很match的函数--> sigmoid
函数式为:
f(x) = \frac{1}{1+e^{-x}}
图像为:
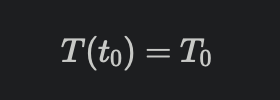
该函数以原点为中心，将实数集映射到值（0，1）且两边都是开区间
我们希望通过平移和拉伸，对于上面的[-15,2]的区间映射做映射,对原点平移$x_0$,再对函数拉伸之后的函数为
f(x) = \frac{1}{1+e^{-\alpha(x-x_0)}}
我们希望当x趋近2的时候，分数接近1，对于终点的取得，我们可以去两个极值的中心 $x_0=(-15+2) / 2 = -6.5$ 然后函数变为
f(x) = \frac{1}{1+e^{-\alpha(x-(-6.5))}}
假设我们代入$f(2) = 0.95$ 可以得到:$\alpha \approx -0.346405$ 函数生成 然后我们还可以检测下-15,我们希望-15大于0且比较小 $f(-15)=\frac{1}{1+e^{-(-0.346405)*(-15-(-6.5))}} \approx 0.04999$
符合要求，然后0-1的分数再乘以100,将其转成0-100的归一分数
